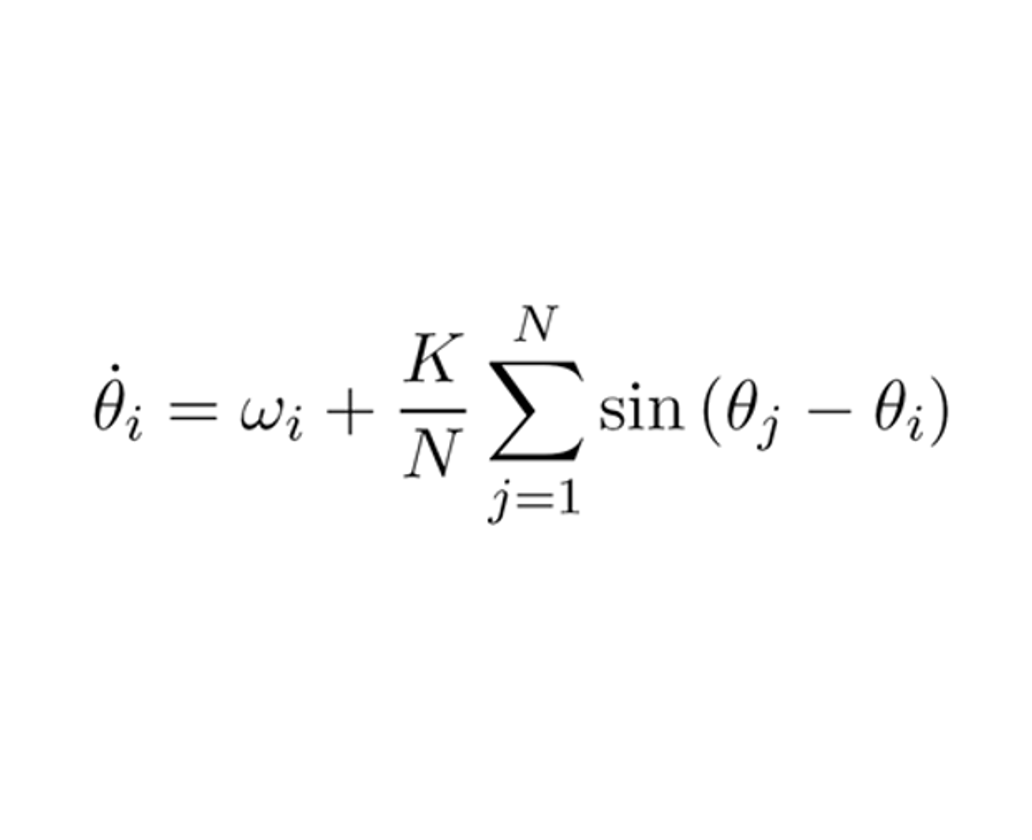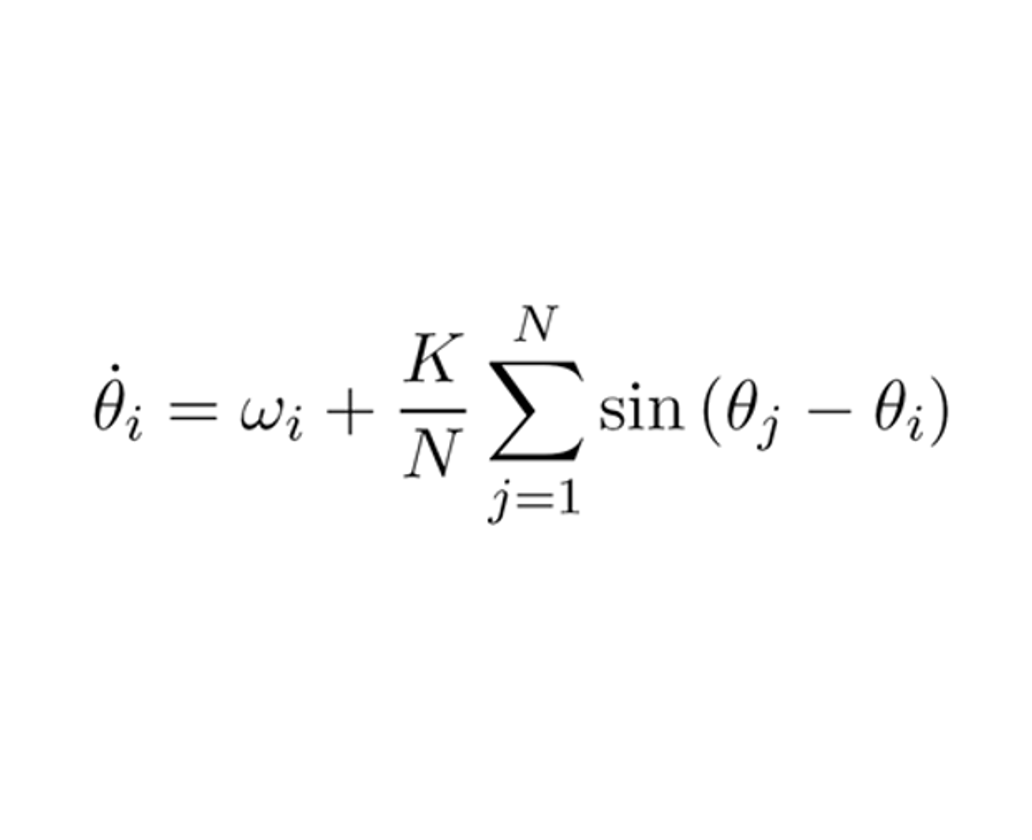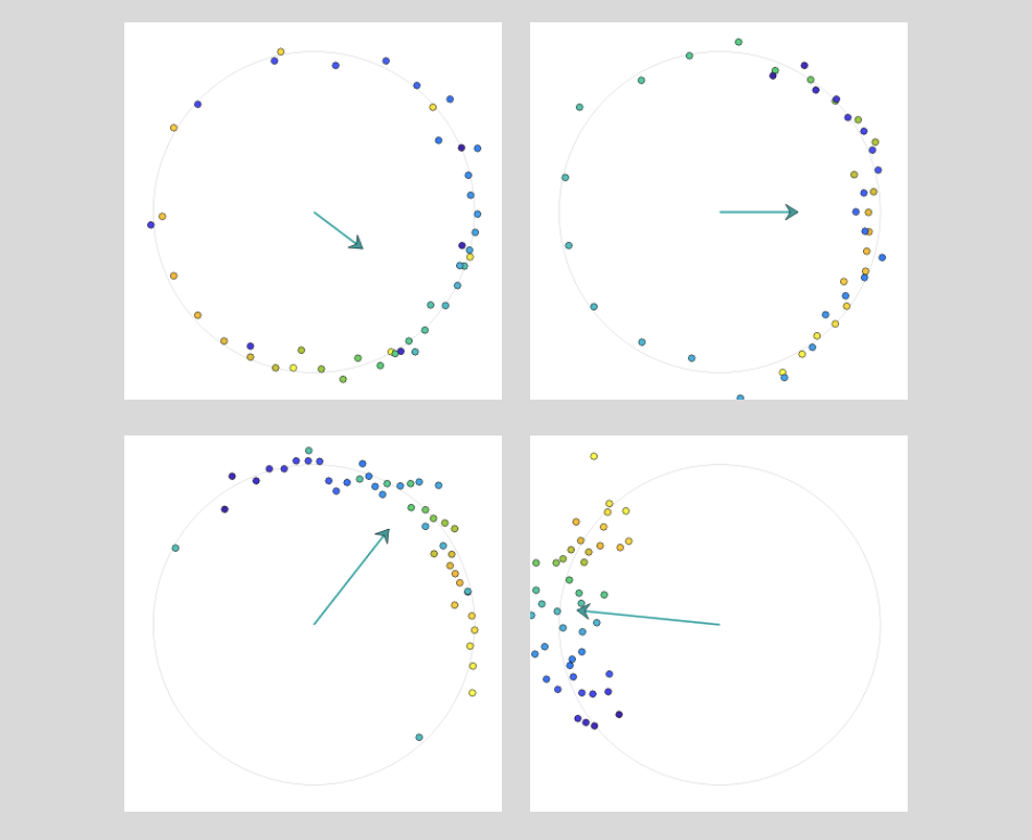
The following is a frame of the simulation created in MATLAB. Each particle orbits a center with an individual period that is lightly coupled with the period of nearby oscillators.

This representation is a simplification of many coupled multi-oscillator systems.

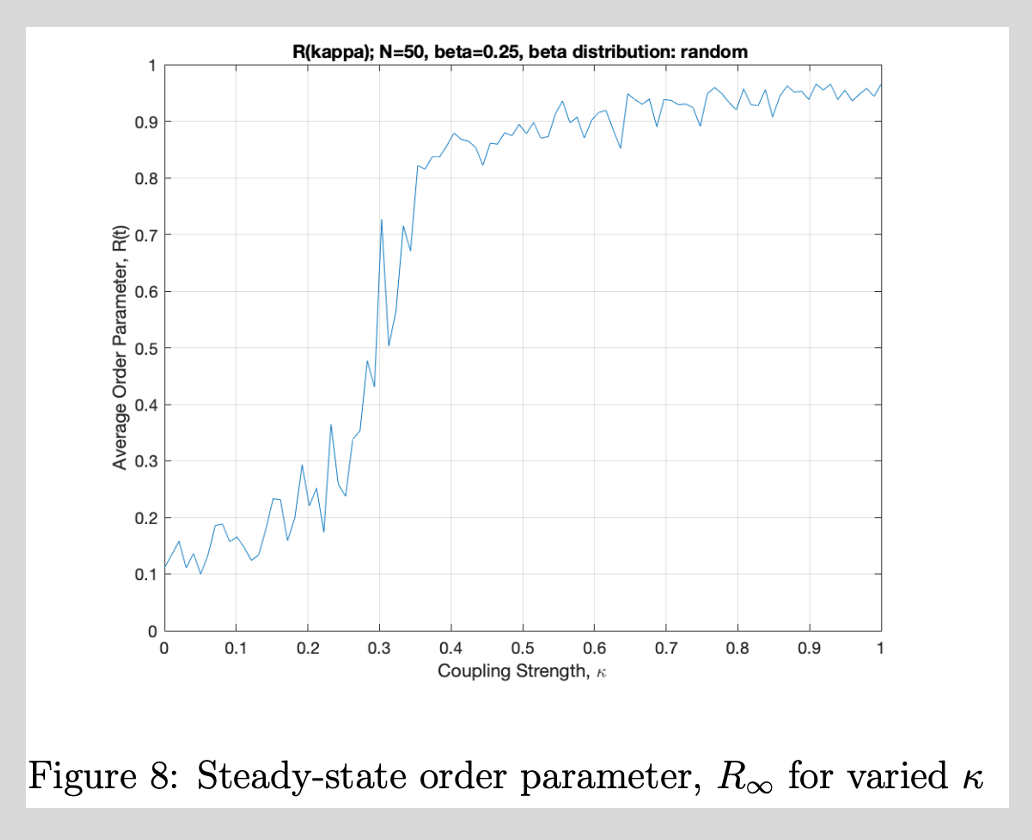
In conducting the analysis, some parameters only influenced synchronization until a threshold. This illustrates the transient behavior of one such parameter as defined by an overall order parameter.

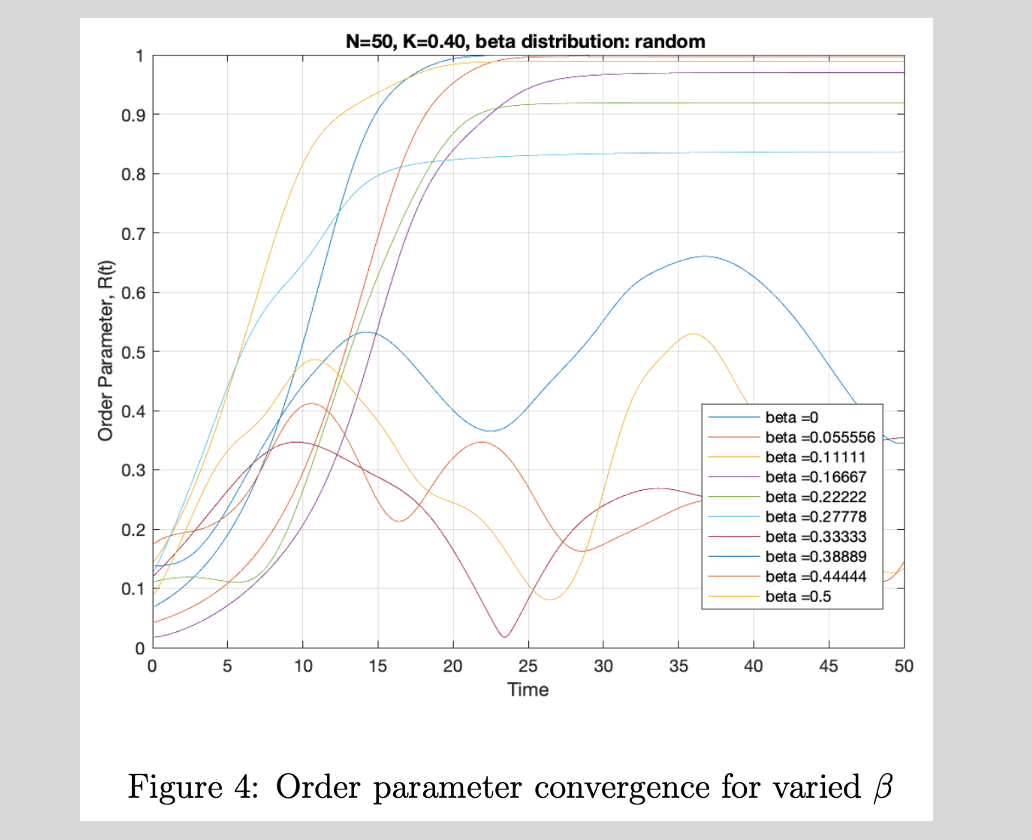
This plot shows the increase in order that accompanies stronger coupling between oscillators, and the interesting relationship between the two features.

This is the Kuramoto equation for coupled oscillators. It describes a change in rotation rate as a function of the sum of individual oscillators coupled with their neighbors.